3.1定点数运算及溢出检测  

定点数加法运算

[X] 补 +[Y] 补 =[X+Y] 补 mod 2 ^(n+1)

算法理解
例1 已知 X=+ 10010 Y= -10101 求X+Y
解: [X] 补 =010010     [Y] 补 =101011
[X+Y] 补 =[X] 补 +[Y] 补 =010010+101011
=111101
所以: X+Y= - 00011

定点数减法运算

[X-Y] 补 =[X] 补 − [Y] 补 =[X] 补 +[− Y] 补

算法理解
例2 已知 [Y] 补 =10011 求 [–Y] 补
解： [Y] 补 =10011
Y= – 1101       -Y= 1101
 [-Y] 补 = 01101
对比 [ Y ] 补 =10011
可知 ： 通过右向左扫描[Y] 补 ， 在遇到数字1及之前，直接输出遇到的数字，
遇到1之后，取反输出，即可得到[-Y] 补 ，反之亦然！

----------------

例3 已知 X=+10101 Y=+ 10010 求X-Y
解: [X] 补 =010101 , [Y] 补 =010010 , [-Y] 补 =101110
[X-Y] 补 =[X] 补 +[-Y] 补 =010101+101110
=1 000011
所以: X - Y=+ 000011

数溢出的概念及其判断方法

1)溢出的概念
运算结果超出了某种数据类型的表示范围。

例4 已知 X=+ 10010 Y= +10101 求X+Y
解: [X] 补 =010010     [Y] 补 = 010101
[X+Y] 补 =[X] 补 +[Y] 补 =010010 + 010101
=100111
所以: X+Y= - 11001
两个正数之和为负数!

-----------

例5 已知 X=- 10010 Y= -10101 求X+Y
解: [X] 补 =101110 [Y] 补 = 101011
[X+Y] 补 =[X] 补 +[Y] 补 = 101110 + 101011
=1 010001
所以: X+Y= + 010001
两个负数之和为正数!

2) 溢出的检测方法
• 溢出只可能发生在同符号数相加时，包括[X] 补 与[Y] 补 ； [X] 补 与[-Y]同号；
(1) 方法1：对操作数和运算结果的符号位进行检测
当结果的符号位与操作数的符号不相同时就表明发生了溢出
(设X0 ，Y0 为参加运算数的符号位， S0 为结果的符号位)

V=X₀Y₀ ! S₀+  ! X₀ !Y₀S₀  

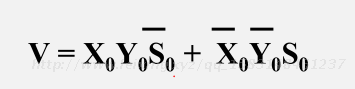
当V=1时，运算结果溢出，根据该逻辑表达式，容易画出相应电路。

(2)方法2：对最高数据位进位和符号进位进行检测

设运算时最高数据位产生的进位为C₁，符号位产生的进位为C₀

溢出检测电路为：V=C₀⊕C₁，这两个不同步时溢出。

(3)方法3：用变型补码

• [X]_补=X_f1X_f2.X₁X₂X₃…X_n mod 2ⁿ⁺²(双符号位) 。（如负数的符号位上是11）
• 模是最高符号位进位位所在的权值。
• 溢出判断：V=X_f1⊕X_f2,只要两个符号位不同，则其发生溢出了。
• 用双符号方式进行运算，运算结果符号位不一致则溢出

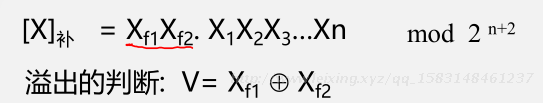
例6 已知 X=- 10010 Y= -10101 求X+Y
解: [X] 补 =1101110 [Y] 补 = 1101011
[X+Y] 补 =[X] 补 +[Y] 补 = 1101110 + 1101011
=1 10 10001

V= 1 ⊕  0 =1 故发生溢出！

(4) 溢出判断的软件方法
int tadd_ok(int x,int y) {
int sum=x+y;
int neg_over=x<0&&y<0&&sum>=0;
int pos_over=x>=0&&y>=0&&sum<0;
return !neg_over&&!pos_over; }
体会软/硬件功能的等效性和差异性！
体会软/硬协同的系统观！

无符号数运算的溢出判断

无符号数加法的溢出可用ALU的进位表示
无符号数减法的溢出也可用带加/减功能的ALU的进位取反后表示。

3.2 定点数补码加、减运算器设计

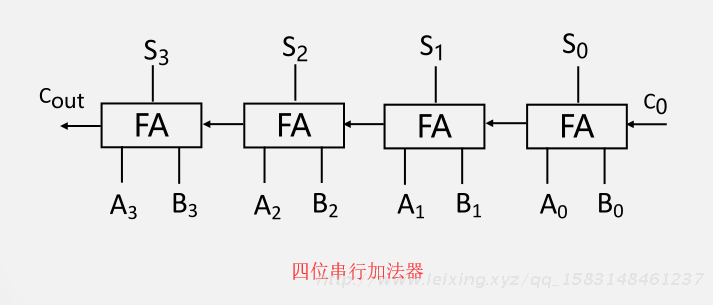
1四位串行加法器的设计（基于一位全加器FA）

一位全加器FA

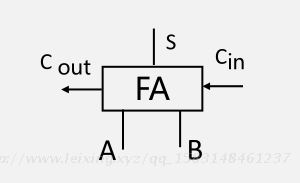
输入端  

A 加数

B 被加数

Cin 相邻低位向本位的进位输入位  Cin

输出端

S 本位和

Cout  本位向相邻高位的的进位输出位Cout

------------

四位串行加法器

设计思路: [X] 补 + [Y] 补 = [X] 补 + [Y] 补

2 四位串行加/减法器设计

设计思路: [X] 补 - [Y] 补 = [X] 补 + [-Y] 补

补码  = 反码 + 1

定点数减法运算

[X-Y] 补 =[X] 补 − [Y] 补 = [X] 补 +[− Y] 补

补码 = 反码 + 1  

算法理解
例2 已知 [Y] 补 =10011 求 [–Y] 补
解： [Y] 补 =10011
Y= – 1101       -Y= 1101
 [-Y] 补 = 01101
对比 [ Y ] 补 =10011
可知 ： 通过右向左扫描[Y] 补 ， 在遇到数字1及之前，直接输出遇到的数字，
遇到1之后，取反输出，即可得到[-Y] 补 ，反之亦然！

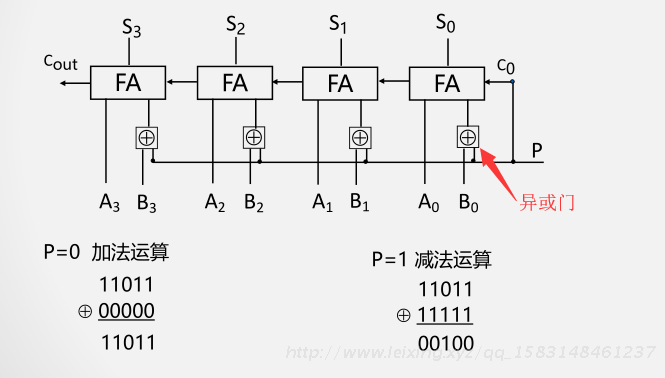
3带溢出检测功能的加/减运算器

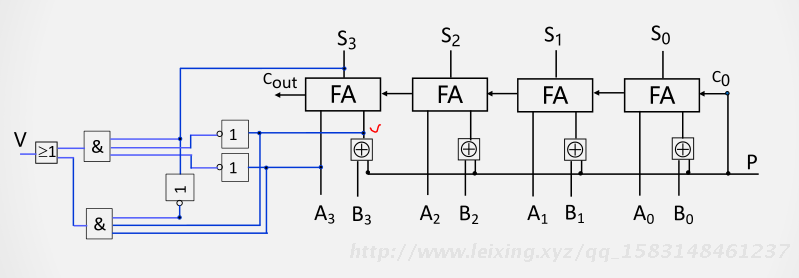
V=X₀Y₀ ! S₀+  ! X₀ !Y₀S₀    

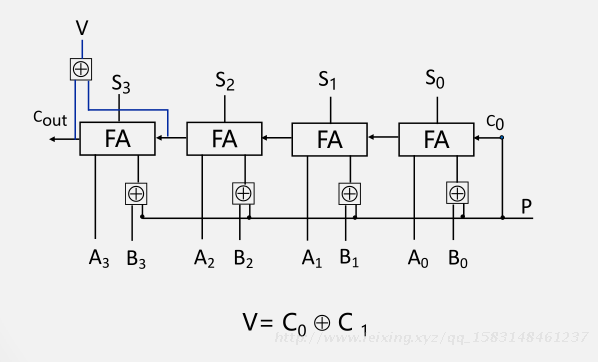
溢出判断：V= C0 ⊕ C1

4 带无符号数溢出检测功能的加/减运算器

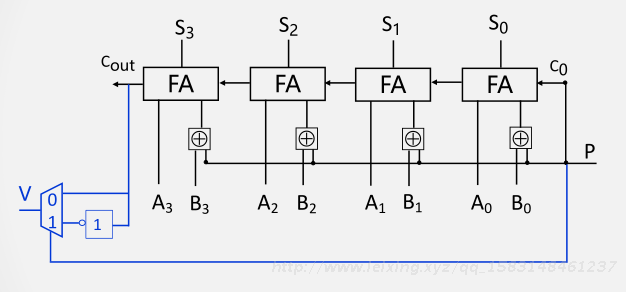
P=1 选择无符号数减法溢出（借位）
P=0时，选择无符号加法溢出（进位）

5 串行进位

串行进位：运算速度慢！

C out = Ai B i + ( B i +A i) C in
C 2 = A 1 B 1 + ( B 1 +A 1 )C 1
C 3 = A 2 B 2 + ( B 2 +A 2 )C 2
C 4 = A 3 B 3 + (B 3 +A 3 )C 3

存在相互之间等待的依存关系  

6并行进位 (先行进位)

C 1 = A 0 B 0 + (B 0 +A 0 )C 0

C 2 = A 1 B 1 + ( B 1 +A 1 )C 1

= A 1 B 1 + (A 1 + B 1 )A0 B 0 + ( A 1 +B 1) ( A 0 +B 0 ) C 0  

C 3 = A 2 B 2 + ( B 2 +A 2 )C 2

= A 2 B 2 +(A 2 +B 2 )(A 1 B 1 + (A 1 +B 1 ) A 0 B 0 )
+ (A 2 +B 2 )( A 1 +B 1 ) (A 0 +B 0 )C 0  

C 4 = A 3 B 3 + (B 3 +A 3 )C 3
=A 3 B 3 +(A 3 +B 3 )(A 2 B 2 +(A 2 +B 2 )(A 1 B 1 + (A 1 +B 1 ) A
0 B 0 )+ (A 3 +B 3 ) (A 2 +B 2 )( A 1 +B 1 ) (A 0 +B 0 )

之间不再有相互等待的依存关系

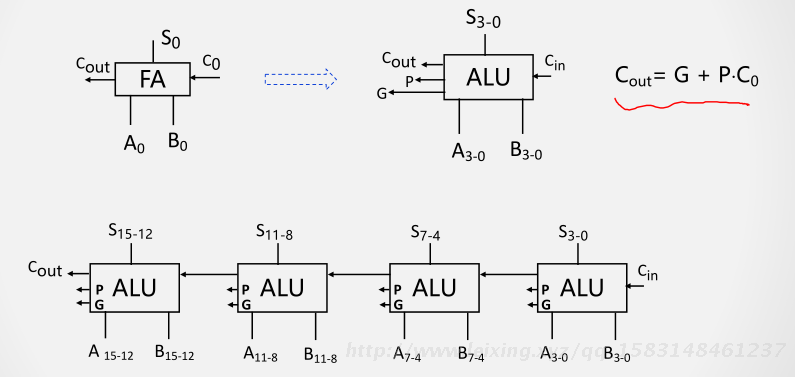
4位并行进位运算器

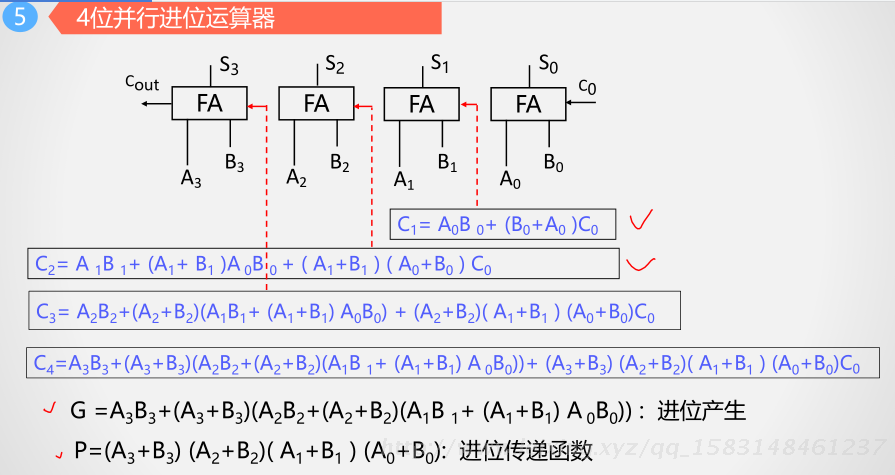
G =A 3 B 3 +(A 3 +B 3 )(A 2 B 2 +(A 2 +B 2 )(A 1 B 1 + (A 1 +B 1 ) A0 B 0 )) : 进位产生
P=(A 3 +B 3 ) (A 2 +B 2 )( A 1 +B 1 ) (A 0 +B 0 ): 进位传递函数

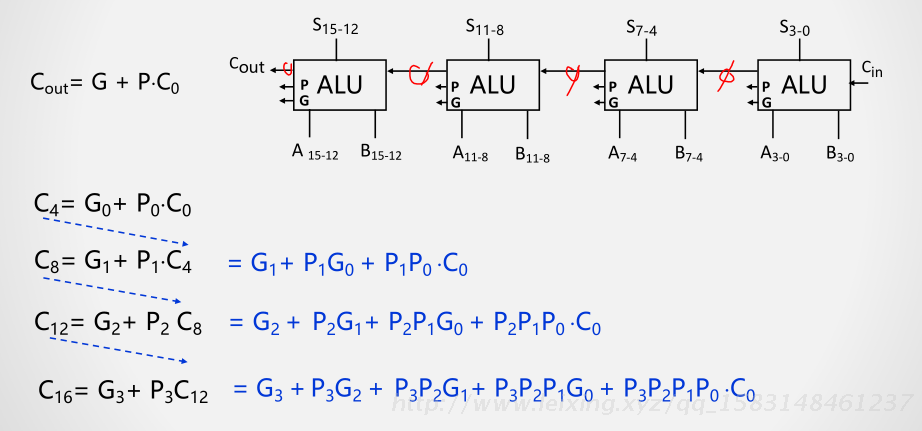
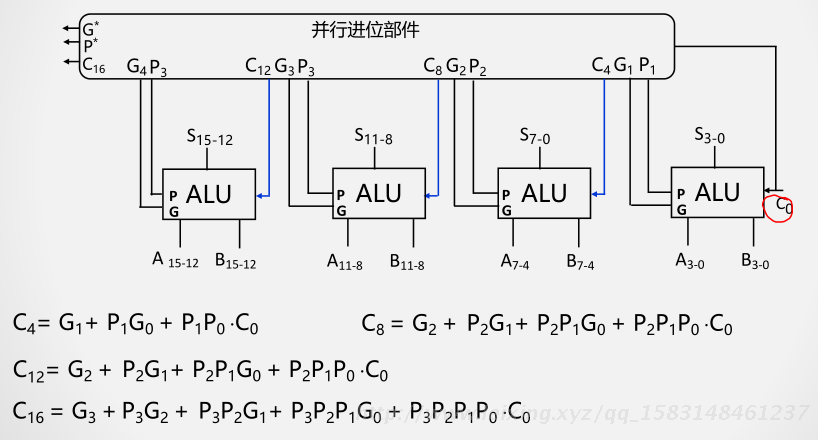
C out = G + P*C 0

多位串行进位与并行进位运算器

3.3 原码一位乘法  

移位操作及其意义

逻辑左移，低位补0
算数左移，低位补0，移动一位相当于乘2
逻辑左移和算数左移一致，但是意义不同。

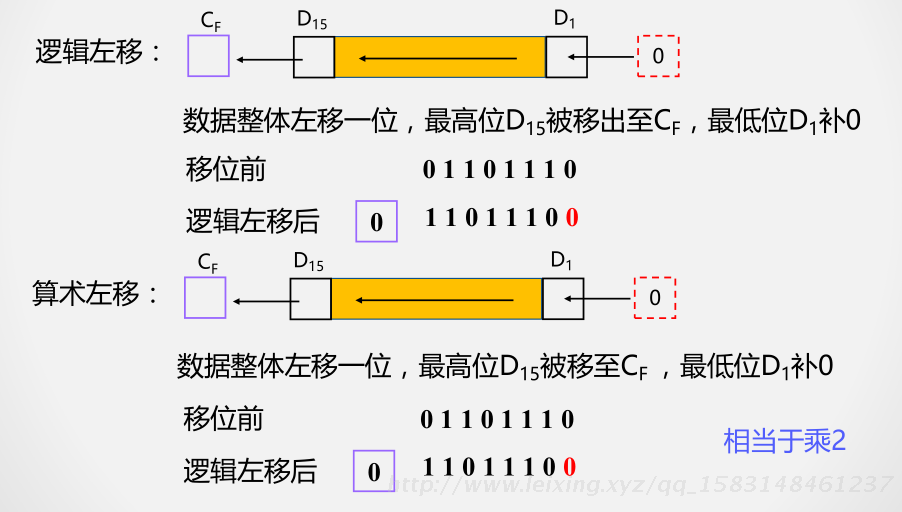
逻辑移动：右移，高位补0
算数移动：右移，高位补原来的，移动一位相当于除2

逻辑左移和算数左移不 一致

二进制乘法的手工计算过程

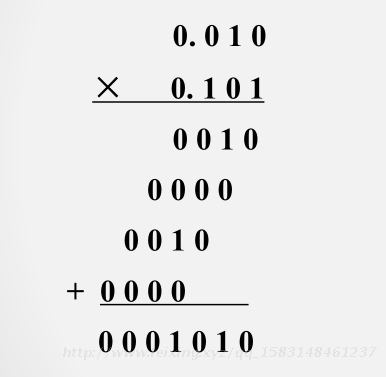
a. 说明乘法可由加法实现
b. 存在的问题：
• 需要多输入的全加器（最多为n+1）;
• 需要长度为2n的积寄存器;
• 对应乘数的不同位，部分积左移次数不同，
且乘法过程中总移位次数多。

如何解决上述问题（改进的方法）

• 需要多输入的全加器（最多为n+1）
基于FA的循环累加0或被乘数。将右移的一位放到乘数寄存器

• 针对乘数不同位部分积左移次数不同的问题
右移部分积！乘数寄存器 

• 需要长度为2n的积寄存器
从部分积和乘数寄存器取结果

原码一位乘法算法

符号位单独参加运算，数据位取绝对值参加运算。

运算法则：
设： [X] 原 =X 0 .X 1 X 2 …X n [Y] 原 =Y 0 . Y 1 Y 2 …Y n
则：P0 = X 0  Y 0 |P| = |X|· |Y|
运算过程采用改进的乘法运算方法。

例1 已知 X = 0.110 Y= - 0.101 用原码一位乘法求X*Y

3.4 补码一位乘法  

1 补码一位乘法的基本方法

设[X] 补 = X 0 X 1 X 2 X 3 …X n [Y] 补 = Y 0 Y 1 Y 2 Y 3 …Y n
可证明：
[X.Y] 补 = [X] 补 •( 0.Y 1 Y 2 Y 3 …Yn ) –Y 0 • [X] 补  

进一步展开合并后可得：

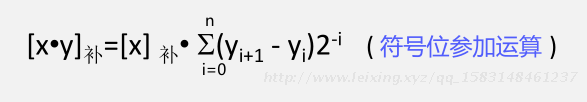
补码一位乘法的运算规则如下:
(1)如果y n+1 =y n ,部分积加0，部分积算术右移1位；
(2)如果y n+1 y n =10,部分积加[x] 补 ，部分积算术右移1位；
(3)如果y n+1 y n =01,部分积加[-x] 补 ，部分积算术右移1位.
重复进行n＋1步，但最后一步不移位。
包括一位符号位，所得乘积为2n＋1位，其中n为数据位位数.

设[X] 补 = X 0 X 1 X 2 X 3 …X n [Y] 补 = Y 0 Y 1 Y 2 Y 3 …Y n

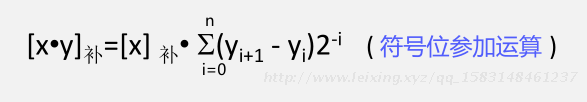
几个特殊问题的处理

(1) i=n时 ,y n+1 = ？     y n+1 = 0  
(2) y n+1 是哪个寄存器？      在乘数寄存器Y后增加的一位  
(3)算术右移的对象有哪些？      部分积和乘数寄存器均右移 

例1 已知X= +1101 Y=+1011 用补码一位乘法求 X*Y

3.5 乘法运算器设计

乘数寄存器

部分积寄存器

3.7浮点数加减运算

由于浮点数是将数据的表示范围与精确度分别表示的数据表示方法，若不对浮点数的表示作出明确规定，同一个浮点数的表示就不唯一，

规格化浮点数是指把一个浮点数按指定的格式进行转换，
以浮点数一般格式为例，规格化浮点数的尾数形式为:

00.1x…x 或 11.0x…x

即：最高有效数据位（小数点后第一位）与符号位不同。

当尾数结果为 00.0x…x 或 11.1xxxx，需要左规格化即将尾数向左移动，
每移动一次，阶码减1，直到尾数形式为 00.1x…x 或 11.0x…x。

浮点数加减运算方法及步骤

设 x = 2^Ex •Mx            y = 2^Ey •My
则： x + y = (2 ^(Ex -Ey) •Mx + My ) + 2 ^ Ey (Ey >= Ex)

1) 对阶
• 求阶差；
• 右移阶码小的浮点数的尾数并同步增加其阶码，直至两数阶码相等。
2 )尾数加/减
尾数加/减运算 （用对阶后的尾数）
3)结果规格化
4)舍入
右移规格化时可能丢失一些低位的数值位, 为提高精度, 可采取舍入的方法:
•0 舍 1 入 : 若右移出的是1则在最低位加1;
•恒置 1 : 只要数字位1被移掉,就将最后一位恒置成1。
5)溢出处理
浮点数的溢出标志: 阶码溢出
• 阶码上溢 ： 阶码的符号位为 01
• 阶码下溢 ： 阶码的符号位为 10

例 设 x = 2 ^010 × 0.11011011            y = 2 ^100 × (- 0.10101100) 求 x+y

解：先用补码形式表示x 和 y
[X] 补 = 00 010 ， 00.11011011
[Y] 补 = 00 100 ，11.01010100

(1) 对阶
[E ]补 =  [Ex] 补 + [ - Ey] 补 = 00010 + 11100 = 11 110  （或运算）

E = – 2   , x 的阶码 小于 y 的阶码
将x 的尾数向右移动2位，同时阶码加 2 ，对阶后的 x 为：

[X] 补 = 00 100 ， 00.0011011011

2)尾数运算
   00.00110110 11
+ 11.01010100

---------------------------------------------
   11.1000101011