计算机组成原理复习
中国大学MOOC中华中科技大学秦磊华教授的《计算机组成原理》慕课
参考书 计算机组成原理 第5版
第一章 计算机系统概论
1.1 冯·诺依曼结构计算机工作原理及层次结构分析
冯·诺依曼,因提出“离散变量自动电子计算机方案”-EDVAC (Electronic Discrete Variable Automatic Computer ) ,被称为 “计算机之父”,该方案至今仍为计算机设计者所遵循;
是20世纪最重要的数学家之一,因其在现代计算机、博弈论等领域的重大贡献成为美国科学院院士。
冯·诺依曼计算机的工作原理
存储程序:将程序存放在计算机的存储器中;
(存储系统构建与快速访问 )
程序控制: 按指令地址访问存储器并取出指令,经译码依次产生指令执行所需的控制信号,实现对计算的控制,完成指令的功能。
(指令系统、控制器设计等)
冯诺依曼型计算机的主要设计思想是:
1、数字计算机的数制采用二进制;
2、计算机应该按照程序顺序执行。
具体内容是:
1.计算机由控制器、运算器、存储器、输入设备、输出设备五大部分组成。
2.程序和数据以二进制代码形式存放在存储器中,存放位置由地址确定。
3.控制器根据存放在存储器中地指令序列(程序)进行工作,并由一个程序计数器控制指令地执行。控制器具有判断能力,能根据计算结果选择不同的工作流程。
根据冯诺依曼体系结构构成的计算机,必须具有如下功能:
1、把需要的程序和数据送至计算机中。
2、必须具有长期记忆程序、数据、中间结果及最终运算结果的能力。
3、能够完成各种算术、逻辑运算和数据传送等数据加工处理的能力。
4、能够根据需要控制程序走向,并能根据指令控制机器的各部件协调操作。
5、能够按照要求将处理结果输出给用户。
为了完成上述的功能,计算机必须具备五大基本组成部件,包括:
1、输入数据和程序的输入设备;
2、记忆程序和数据的存储器;
3、完成数据加工处理的运算器;
4、控制程序执行的控制器;
5、输出处理结果的输出设备 。
冯·诺依曼计算机的组成(硬件+ 软件)
1)硬件系统(总体图)
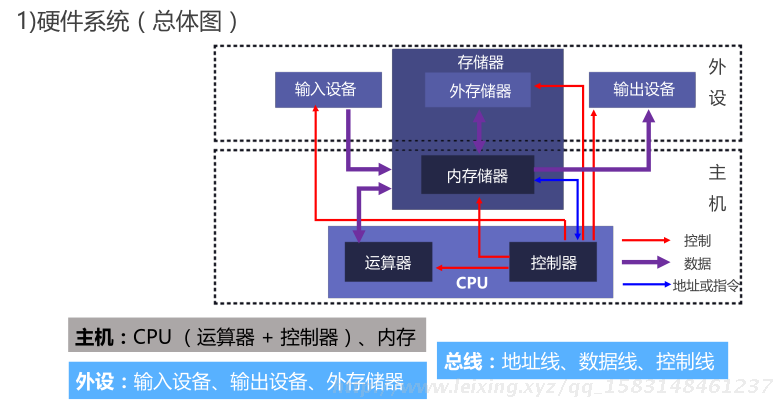
1)硬件系统 - 运算器
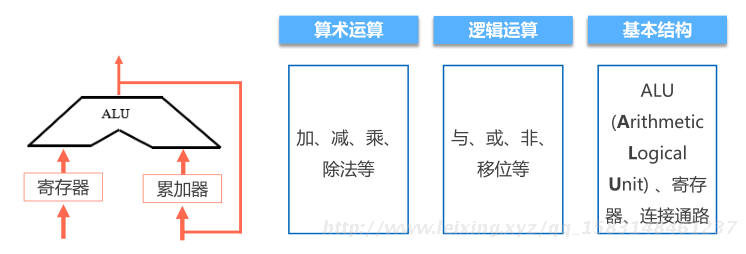
算术运算
加、减、乘、除法等
逻辑运算
与、或、非、移位等
基本结构
ALU(Arithmetic Logical Unit) 、寄存器、连接通路
注重功能与结构的关系?
-- 指令、数据类型、性能要求等等
1)硬件系统 - 控制器
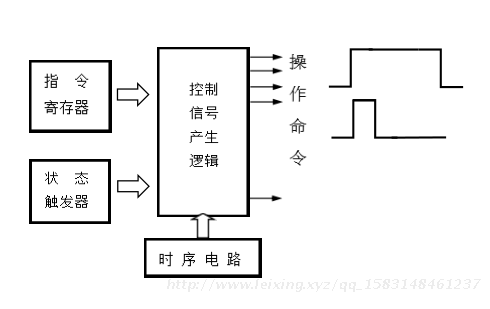
基本功能
产生指令执行过程所需要的所有控制信号,控制相关功能部件执行相应操作;
控制信号的产生方式
微程序、
硬布线。
控制信号的形式
电平信号、
脉冲信号;
产生控制信号的
依据
指令、状态、
时序;
1)硬件系统 - 存储器
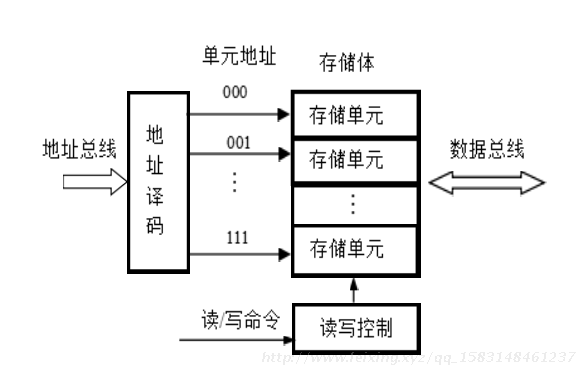
功能
存储原程序、
原数据、运算
中间结果
工作模式
读/写;
工作原理
按地址访问,
读/写数据。
容量与地址线数量
容量 → 地址线数量
1K → 10
1M → 20
1G → 30
--------------------
一根地址线是1和0两种状态,可以表示2个地址0和1。2根呢就是00,01,10,11,四种状态,可以用来表示4个地址。n根线,就可以有2的n次方种状态,可以表示2的n次方个地址。
一根地址总线寻址为2^1=2,10根地址总线就是2^10=1024Byte=1KB,13根就是2^13=8KB。N根就是2^N。
1KB=1024B,8KB=1024B*8=2^N,N=13
--------------------
1KB=2^10B 需要10根地址总线
1MB =2^10KB = 2^10*2^10B =2^20B 需要20根地址总线
1GB=2^10MB=2^10*2^10*2^10B =2^30B 需要30根地址总线
2GB=2 *2^3B=2^31b需要31根地址总线
256GB=2^8 * 2^30B = 2^38B
-------------------
1024Byte(字节)=1KB
1024kB=1MB
1024MB=1GB
1024=2^10
--------------------
1)硬件系统 -输入/输出设备
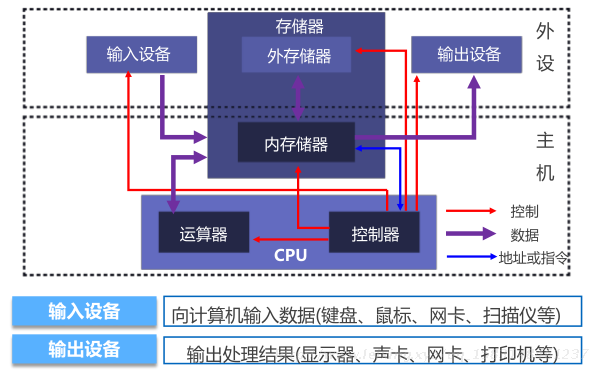
输入设备
向计算机输入数据(键盘、鼠标、网卡、扫描仪等)
输出设备
输出处理结果(显示器、声卡、网卡、打印机等)
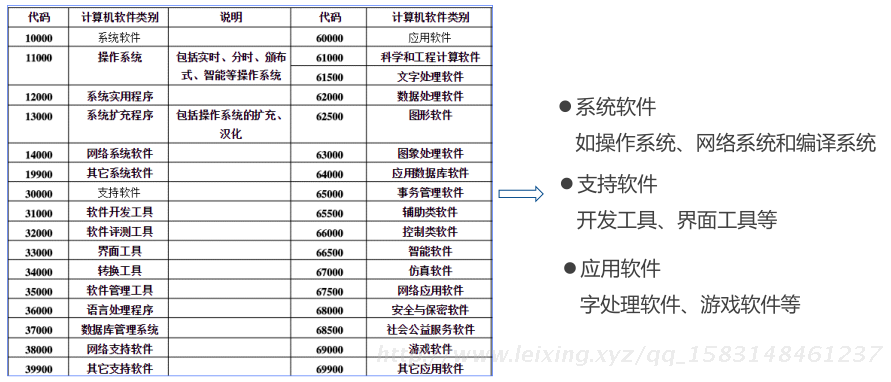
2) 软件系统
软件的理解
⚫可运行的思想和内容的数字化
思想:算法、规律、方法---程序表达
内容:图形、图像、数据、声音、文字等被处理的对象
⚫软件的表现形式: 程序和数据(以二进制表示的信息)
⚫软件的核心: 算法
3) 硬件与软件系统间的关系
相互依存
硬件是软件运行的基础,软件的正常运行是硬件发挥作用的重要途径。计算机系统必须要配备完善的软件系统才能正常工作,且应充分发挥其硬件的功能;
逻辑等效性
某些功能既可由硬件实现,也可由软件来实现;
协同发展
软件随硬件技术的迅速发展而发展,而软件的不断发展与完善又促进硬件的更新,两者密切地交织发展,缺一不可 。
应用程序
高级语言 (e.g., C)
汇编语言 (e.g., MIPS)
操作系统
指令集架构层 (e.g., MIPS)
微代码层
Compiler(翻译)
硬件逻辑层
1.2计算机的性能指标P5
非时间指标
1、机器字长:志及其一次性能处理的二进制位数;
ALU算术逻辑单元(arithmetic and logic unit) 是能实现多组算术运算和逻辑运算的组合逻辑电路,简称ALU。
2、总线宽度:总线一次能并行传送的最大信息位数;
一般指运算器与存储器之间的数据总线位数。
有些计算机内部与尾部数据总线宽度不一致;
Pentium外总线64位,内总线32位(两条32位流水线)
3、主存容量与存储带宽
主存容量:是指一台计算机主存所包含的存储丹云总数。
存储带宽:指单位时间内与主存交换的二进制信息量,常用B/s(字节/秒)。(影响存储带宽的指标包括数据位宽和数据传输速率)。
时间指标
1、主频f/时钟周期T,外频、倍频
主频f
指CPU内核工作的始终频率,即CPU内数字脉冲信号震荡的速率,与CPU实际的运算能力不是唯一的、直接关系。
时钟周期T,也称节拍周期,是计算机中最基本的最小的时间单位。在一个时间周期内,CPU 仅完成一个最基本的动作。
f与T的关系
互为倒数,f越高,T就越小(f=100MHz时,T=10ns; f=1GHz时,T=1ns)
频率的倒数即是周期,即1/HZ=1s;
100MHz=100 * 10^6 Hz = 10^8 Hz
T = 1/f = 1/10^8 = 10^(-8)s = 10^(-5) ms = 10^(-2)μs = 10^(1)ns = 10ns
即频率是100MHZ时,其周期是10ns纳秒
外频
指CPU(内存)与主板之间同步的始终频率;
倍频
CPU主频f与外频之间的倍数。
主频f = 外频 * 倍频
如: 奔腾Pentium 4 2.4G CPU主频
2.4G = 2400M = 133M(外频)* 18(倍频)
CPI (Clock cycles Per Instruction)
执行一条指令(平均)需要的时钟周期数 (即T周期的个数)
单条指令 CPI、一段程序中所有的CPI、指令系统的CPI等。
CPI = 程序中所有指令的时钟周期数之和 / 程序中指令总数
= 求和符号(程序中各类指令的CPI * 程序中该类指令的比例)
MIPS(Million Instruction Per Second)
每秒CPU能执行的指令总条数。(单位:百万条 / 秒)
MIPS = 指令条数 / (执行时间 *10^6)
= 指令条数 / ((所有指令CPU时钟周期数之和 / f)* 10^6 )
= f / (CPI * 10^6) (全性能公式)

CPU时间
执行一段程序所需要的时间
(CPU时间 + I/O时间 + 存储访问时间 + 各类排序时延的等)
CPU时间 = 程序中所有指令的时钟周期数之和 * T
= 程序中所有指令的时钟周期数之和 / f
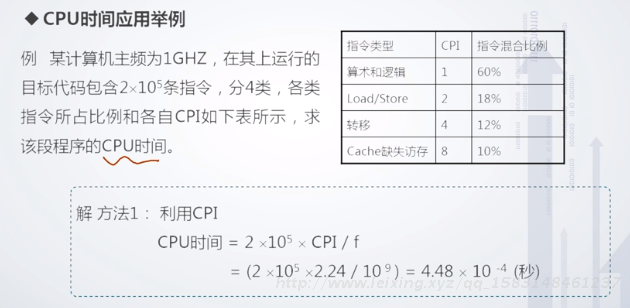
CPU时间的计算方法
1、考虑CPI后的CPU时间
CPU时间 = 总指令数 * CPI * T 时钟周期时间
= 总指令数 * CPI / f 主频
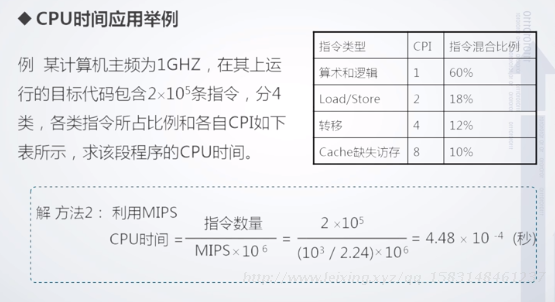
2、考虑MIPS后的CPU时间
CPU时间 = 指令条数 / (执行时间 *10^6)
1.3 计算机性能测试
性能测试的目的
全面了解所测试计算机的性能;
实时掌握计算机的工作状态;
为对比、评估、维护提供依据;
测试的基本原理
计算机系统中配置了大量的传感器和寄存器,系统运行的相关
参数保存在对应的寄存器中;
通过图形/数据方式显示获取的状态数值;
测试程序通过读取相应寄存器的值得到系统运行的状况;
第二章 数据表示
数据表示 原码、反码、补码、移码、定点数、 浮点数IEEE754有32位和64位运算,加减乘除
2.2 定点与浮点数据表示
1 定点数据表示
可表示定点小数和整数
定点数据表示数的不足:数据表示范围受限
2 浮点数据表示
浮点数的使用场合:当数的表示范围超出了定点数能表示的范围时。
把数的范围和精度分别表示的一种数据表示方法。
(1)格式(一般格式)
| Es | E1E2E3……En | Ms | M1M2M3M4 ..Mk | --> | 2^e •m |
|---|

E: 阶码位数,决定数据的范围
M: 尾数位数,决定数的精度
例1:将二进制数x =2^(-01) ×(- 0.1110) 表示成机器形式。假定用8位表示该数,且阶码占3位,尾数占5位(均包含一位符号位)。
解:假定阶码和尾数均采用补码
e=-1 补码 111
m=-0.1110 补码 10010 (1.0010 隐含的点,定点小数)
1 1 1 1 0 0 1 0
不同系统可能根据自己的浮点数格式从中提取不同位数的阶码。所以指定了IEEE 754格式。
IEEE 754格式
IEEE 754格式
| 符号位S | 8位偏指数E | 23位有效尾数M | 单精度 |
|---|---|---|---|
| 符号位S | 11位偏指数E | 52位有效尾数M | 双精度 |
- 指数E采用偏移值,其中单精度偏移值为127,双精度为1023, (为什么对阶码做移位?为了方便把阶码的值变成非负数), 将浮点数的阶码值变成非负整数,便于浮点数的比较和排序。
- IEEE754尾数M形式为1.XXXXXX,其中M部分保存的是XXXXXX(1被隐藏),从而可保留更多的有效位,提高数据表示的精确度。( 单精度和双精度 有效尾数M 都不是完整保存。从计算机中提取一个数据还原成真值的时候,要把1放到M的前面。)
| 精度 | 阶 | 移码 | 二进制表示 |
|---|---|---|---|
| 单精度 | 8 | 127 | 0111 1111 |
| 双精度 | 11 | 1023 | 011 1111 1111 |
| 长双精度 | 15 | 16383 | 011 1111 1111 1111 |
例1.某二进制数 X = + 1.100001* 2^8 , 若要变换成IEEE 754浮点数格式,则对尾数而言需要保存( ),其余位补0即可(说明:只需要填写6位二进制数)
答案:100001
例2.某二进制数 X = + 1.100001* 2^8 ,假定用8位表示该数,且阶码占3位,尾数占5位(均包含一位符号位)。
解:假定阶码和尾数均采用补码
e=8 补码 0100
m=+1.00001 补码 100001 ( 1.00001 隐含的点,定点小数)
0 1 0 0 1 0 0 0 0 1
纯负小数的补码
纯小数补码也就是说系统规定为8位,当位数不够的时候,要在最低有效数后面用0补齐,然后再求它的原码、反码、和补码。
纯小数在求它的原码、反码、和补码时方法和整数是一样的。
例如:X=-0.1011 系统要是规定为8位,那么它的原码为
[x]原=1.1011000 [x]反=1.0100111 [x]补=1.0101000
浮点数据表示
| S | 8位偏指数E | 23位有效尾数M | 单精度 |
|---|
与上述IEEE754格式相对应的32位浮点数的真值可表示为:
N = (-1)^ S * 2 ^(E-127) * 1.M
E-127 在保存的时候,加了127。
随E和M的取值不同,IEEE754浮点数据表示具有不同的意义
浮点数据表示
E=0 , M =0 :表示机器零;
E=0 , M !=0 :则N = (-1)^S * 2 ^(-126) * 0.M,非规格化的浮点数;
1<= E <= 254 :N = (-1)^S * 2^(E-127) * 1.M ,规格化的浮点数;
E=255 , M =0 :无穷大的数,对应于x / 0 (其中x != 0) ;
E=255 , M != 0 :N= NaN,表示一个非数值,对应于0 / 0。
可参考
关于浮点异常,见Kahan教授的《Lecture Notes on IEEE 754》
http://www.cs.berkeley.edu/~wkahan/ 有时打不开
IEEE754 32位浮点数与对应真值之间的变换流程
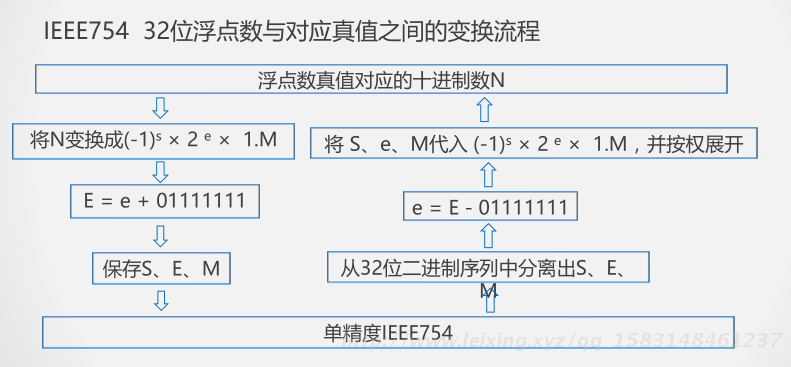
E = e + 01111111 保存的时候,加127。
e = E - 01111111 求真值的时候,减127。
转换成32位IEEE754格式
例1.将十进制数20.59375转换成32位IEEE754格式浮点数的二进制格式(补码)。
解: 先将十进制数换成二进制数:
20.59375(10) = 10100.10011(2)
移动小数点,使其变成1.M的形式
10100.10011 = (-1)^0 * 1. 010010011 * 2^4
S=0, e=4, M = 010010011,
E=100 + 01111111 =10000011
最后得到32位浮点数的二进制存储格式为:
依次保存 SEM
| S | 8位偏指数E | 23位有效尾数M(不够的补0) |
|---|---|---|
| 0 | 10000011 | 01001001100000000000000 |
0100 0001 1010 0100 1100 0000 0000 0000
化成16进制 = 41A4C000H
例2.将单精度32位IEEE754格式的二进制数 0100 0001 1010 0100 1100 0000 0000 0000 转换成真值。
解: 从32位二进制序列中分离出S、E、M
S=0, E=1000 0011 , M = 0100 1001 1,
e=E-127 = 1000 0011 - 01111111 = 100
(-1)^0 * 1. 010010011 * 2^4
= 10100.10011(2)
= 20.59375(10)
2.3 数据校验的基本原理
数据校验的必要性
受元器件的质量、电路故障或噪音干扰等因素的影响,数据在被处理、传输、存储的过程中可能出现错误;
若能设计硬件层面的错误检测机制,可以减少基于软件检错的代价(系统观)。
校验的基本原理
增加冗余码(校验位)
| 有效信息(k位) | 校验信息(r位) |
|---|
码距的概念
同一编码中,任意两个合法编码之间不同二进数位数的最小值;
例 0011与0001 的码距为1,一位错误时无法识别;
0000、0011、0101、0110、1001、1010、1100、1111等编码码距为2。任何一位发生改变,如0000变成1000就从有效编码变成了无效编码,容易检测到这种错误。校验码中增加冗余项的目的就是为了增大码距。
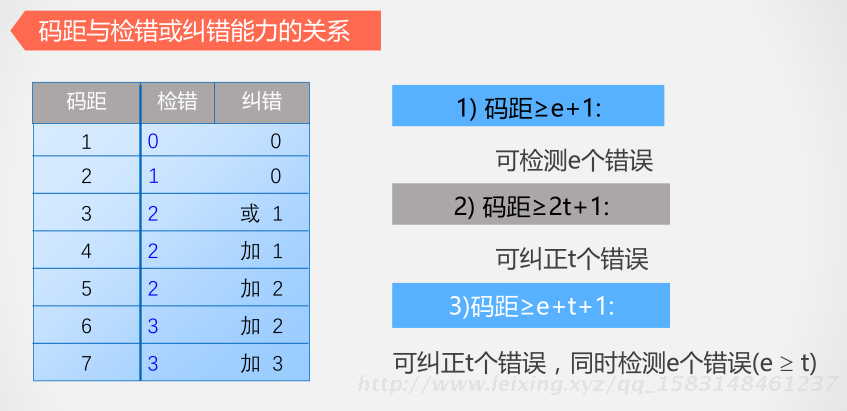
码距与检错或纠错能力的关系
1) 码距≥e+1:
可检测e个错误
2) 码距≥2t+1:
可纠正t个错误
3)码距≥e+t+1:
可纠正t个错误,同时检测e个错误(e≥ t)
选择码距要考虑的因素
| 有效信息(k位) | 校验信息(r位) |
|---|
码距越大,抗干扰能力越强,纠错能力越强,数据冗余越大,编码效率低,编码电路也相对复杂;
选择码距必须考虑信息发生差错的概率和系统能容许的最小差错率。
2.3 奇偶校验
奇偶校验的基本原理
1)增加冗余码(校验位)
| 有效信息(k位) | 校验信息(r位) |
|---|
2)编码:根据有效信息计算校验信息位,使校验码(数据+1位校验信息)中1的个数满足奇/偶校验的要求
0001 --> 00011 (偶校验)
0001
--> 00010 (奇校验)

3)检错方法与电路
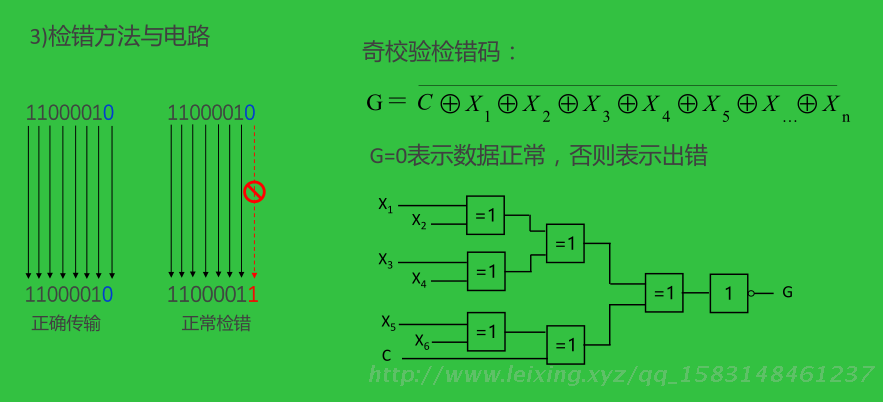
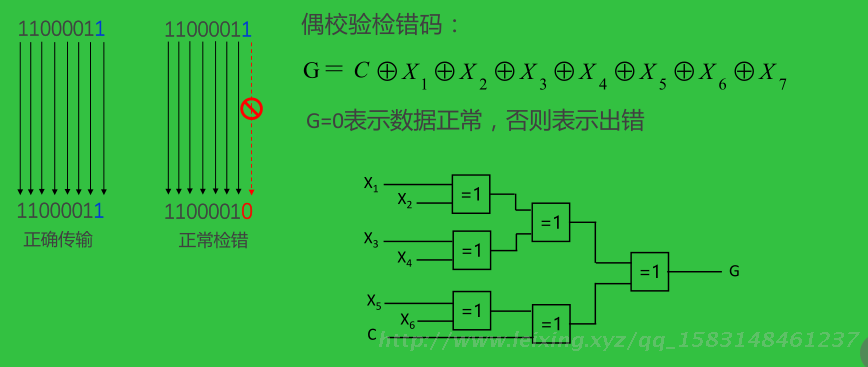
奇偶校验的特点
编码与检错简单
编码效率高
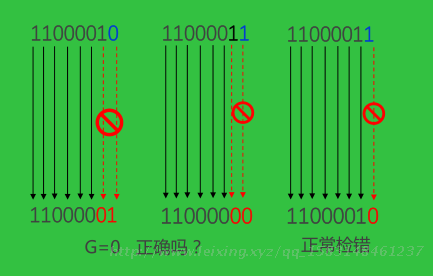
不能检测偶数位错误, 无错结论不可靠,是一种错误检测码
不能定位错误,因此不具备纠错能力
奇偶校验的码距
举例说明奇/偶校验码距为 2
11000011 --> 01000010
改进的奇偶校验
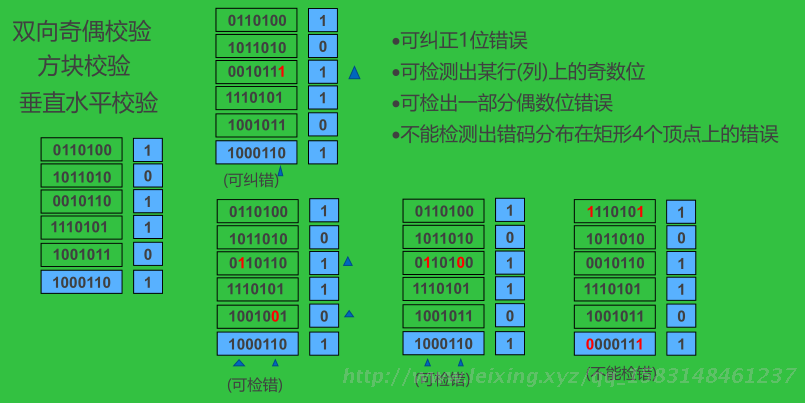
双向奇偶校验
方块校验
垂直水平校验
可纠正1位错误
可检测出某行(列)上的奇数位
可检出一部分偶数位错误
不能检测出错码分布在矩形4个顶点上的错误
哪些场合应用奇偶校验?
工程上的应用
哪条内存条具有错奇偶校验功能的内存条?
http://www.eepw.com.cn/article/280413.htm (关于串口奇偶校验配置的经验)
一般在同步传输方式中常采用奇校验,异步传输方式中常采用偶校验
2.5 CRC校验及其实现
CRC校验的基本原理
增加冗余码(校验位)
| 有效信息(k位) | 校验信息(r位) |
|---|
N=k+r ≤ 2 r -1
生成多项式G(x)
收发双方约定的一个(r + 1)位二进制数,发送方利用G(X)对信息多项式做模2除运算,生成校验
码。接收方利用G(X)对收到的编码多项式做模2除运算检测差错及错误定位。
G(x)应满足的条件
A、最高位和最低位必须为1;
B、当被传送信息(CRC码)任何一位发生错误时,被生成多项式做除后应该使余数不为0;
C、不同位发生错误时,模2除运算后余数不同;
D、对不为0余数继续进行模2除运算应使余数循环。
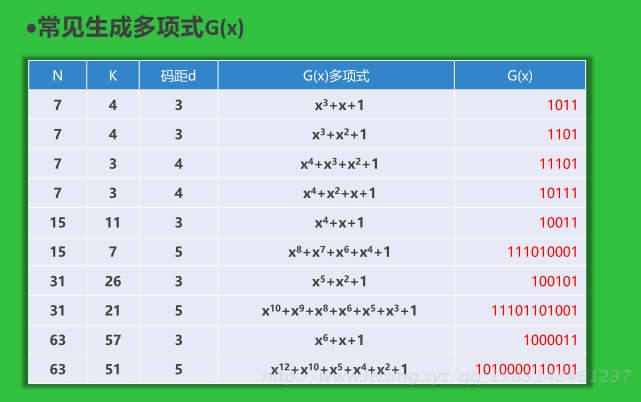
常见生成多项式G(x)
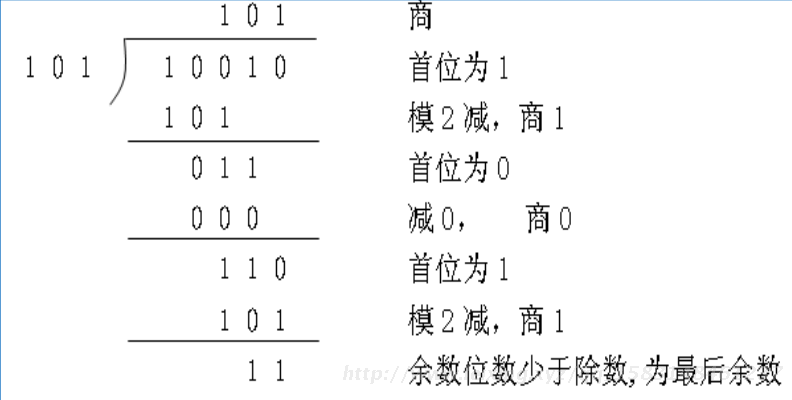
模2除运算
a)加/减运算 (异或运算,加不进位,减不借位)
0±0=0,0±1=1,1±0=1,1±1=0
b)模2除法
按模2减,求部分余数,不借位。
c)上商原则
①部分余数首位为1时,商为1,减除数;
②部分余数首位为0时,商为0,减0;
③当部分余数的位数小于除数的位数时,该余数即为最后余数。
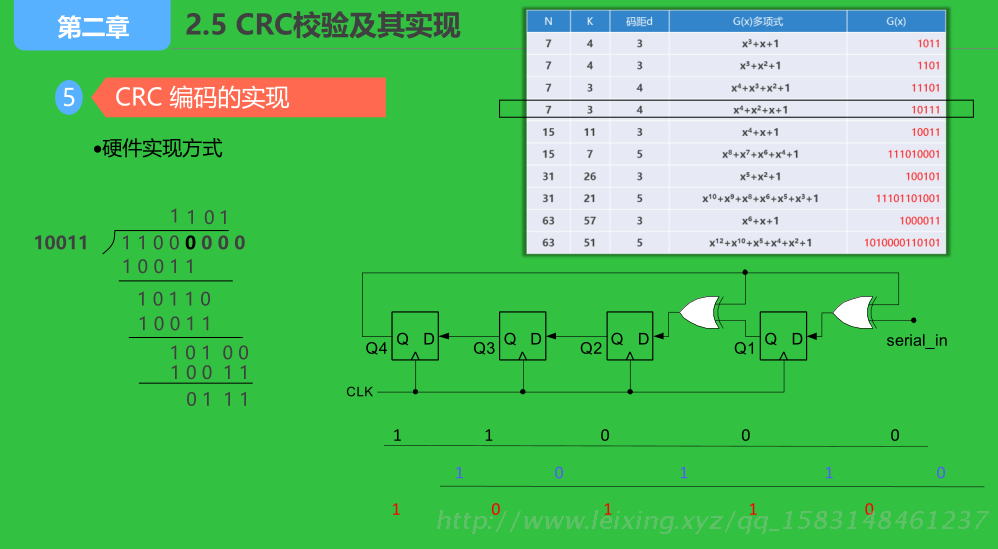
CRC 编码方法
(1)根据待校验信息的长度k,按照 k+r ≤ 2 r -1 确定校验位r的位数
(2)根据r 和生成多项式的选择原则,选择位数为 r +1 的生成多项式G(X)= 1011
如对4位信息 1100 进行CRC编码,根据 4+r ≤ 2 r -1
得 r min = 3
(3)进行下列变化
| 有效信息(k位) | 校验信息(r位) |
|---|
==》1100 000
即:将待校验的二进制信息Q(X)逻辑左移 r 位,得到Q(X)’
CRC编码
(4)对Q(X)’按模2运算法则除G(x),求CRC编码中的r位校验信息
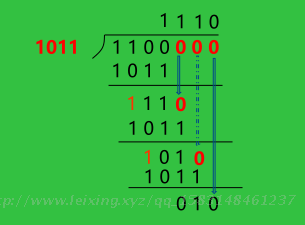
(5)用得到的余数替换Q(X)’的最后r位即可得到对应的CRC编码
1100 000 ==> 1100 010 即为1100 的CRC 编码
CRC的检错与纠错
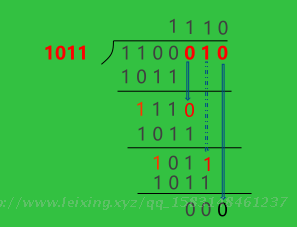
余数为0说明传输没有错误
接收方利用G(X)对收到的有错编码多项式做模2除运算
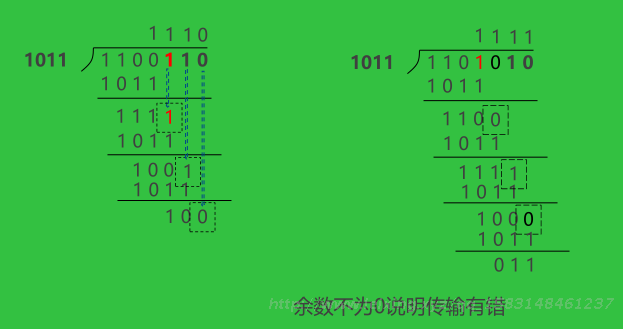
余数不为0说明传输有错。不同位数出错,得到的余数不一样。
编码不同数位出错对应的余数
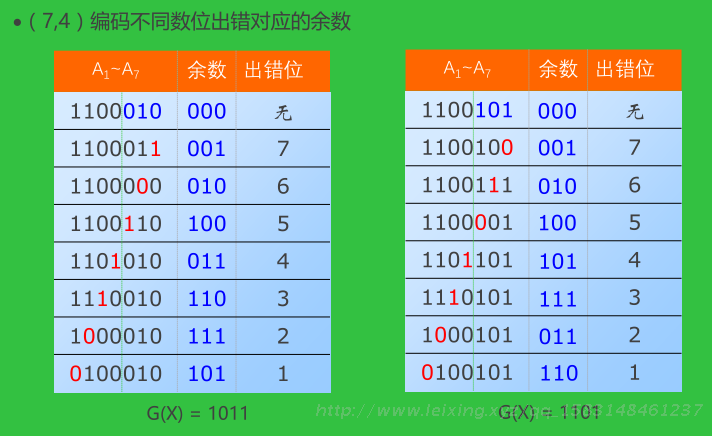
利用出错情况下余数的循环特性进行纠错
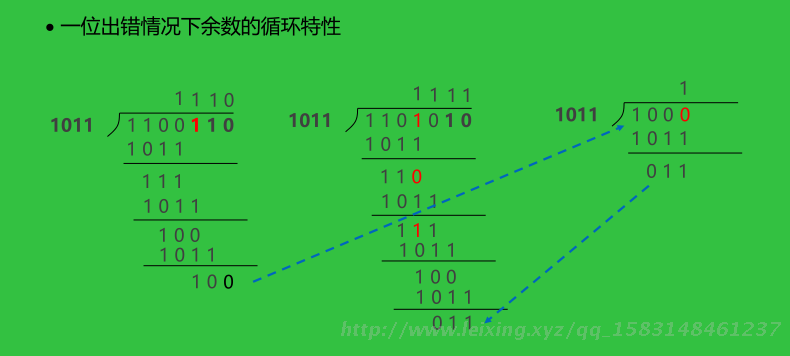
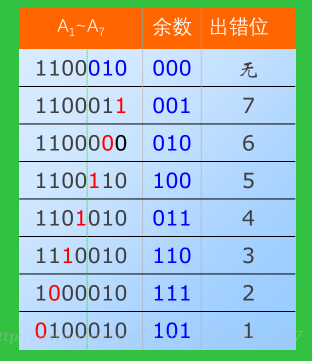
若余数不为0,一边对余数补0继续做模2除,同时让被检测的校验码循环左移,当余数为101时,出错位也移到A1位置。通过异运算纠正后继续循环左移和执行余数模2除法,直到修改后的出错位回原位。不需对每一位提供纠正电路。当位数增多时,循环码校验能有效地降低硬件
代价,这是它得以广泛应用的主要原因。
2.6 海明校验及其实现
增加冗余码(校验位)
| 有效信息(k位) | 校验信息(r位) |
|---|
N=k+r ≤ 2^ r -1
1) 设k+r位海明码从左到右依次为第1,2,3,…..., k+r位,r位校验位记为P i (i=1,2,…,r),分别位于k+r位海明编码的第2 i-1 (i=1,2,…,r)位上,其余位依次放置被校验的数据位;
2) (7,4)海明校验码中校验位和被校验信息位的排列如下:



