按下述两种解决冲突的方法构造哈希表， 原创

设哈希函数H（K）=3 K mod 11，哈希地址空间为0～10，对关键字序列（32，13，49，24，38，21，4，12），按下述两种解决冲突的方法构造哈希表，并分别求出等概率下查找成功时和查找失败时的平均查找长度ASLsucc和ASLunsucc。

① 线性探测法；

② 链地址法。

①

ASL_succ =（1+1+1+2+1+2+1+2）/8=11/8

ASL_unsucc=（1+2+1+8+7+6+5+4+3+2+1）/11=40/11

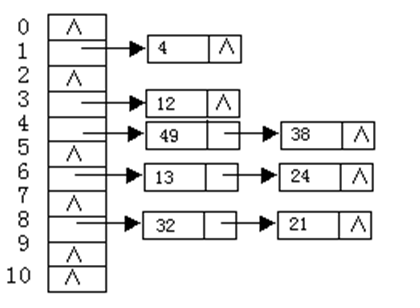
ASL_succ =（1*5+2*3）/8=11/8

ASL_unsucc=（1+2+1+2+3+1+3+1+3+1+1）/11=19/11

最终的插入结果如下表所示：

求查找成功的平均查找长度
查找7，H(7) = 0，在0的位置，一下子就找到了7，查找长度为1。
查找8，H(8) = 3，在3的位置，一下子就找到了8，查找长度为1。
查找30，H(30) = 6，在6的位置，一下子就找到了30，查找长度为1。
查找11，H(11) = 5，在5的位置，一下子就找到了11，查找长度为1。
查找18，H(18) = 5，第一次在5的位置没有找到18，第二次往后挪移一位到6的位置，仍没有找到，第三次再往后挪移一位到7的位置，找到了，查找长度为3。
查找9，H(9) = 6，第一次在6的位置没找到9，第二次往后挪移一位到7的位置，仍没有找到，第三次再往后挪移一位到8的位置，找到了，查找长度为3.
查找14，H(14) = 0，第一次在0的位置没找到14，第二次往后挪移一位到1的位置，找到了，查找长度为2。

所以，查找成功的平均查找长度为(1 + 1 + 1 + 1 + 3 + 3 + 2) / 7 = 12 / 7。

求查找不成功的平均查找长度
查找不成功，说明要查找的数字肯定不在上述的散列表中。
因为这里哈希函数的模为7，所以要查找的数的初始地址只可能位于0~6的位置上。
地址0，到第一个关键字为空的地址2需要比较3次，因此查找不成功的次数为3。比如要查找的数为28，H(28) = (28 * 3) % 7 = 0。即28对应的地址是0，由于存放在0位置的数是7，所以往后挪移一位，发现在1位置存放的数是14，继续往后挪一位，发现位置2上没有数。至此就知道28不在这个哈希表里，即查找28失败。
地址1，到第一个关键字为空的地址2需要比较2次，因此查找不成功的次数为2。
地址2，到第一个关键字为空的地址2需要比较1次，因此查找不成功的次数为1。
地址3，到第一个关键字为空的地址4需要比较2次，因此查找不成功的次数为2。
地址4，到第一个关键字为空的地址4需要比较1次，因此查找不成功的次数为1。
地址5，到第一个关键字为空的地址9需要比较5次，因此查找不成功的次数为5。
比如要查找的数为4，H(4) = (4 * 3) % 7 = 5，所以从地址5开始查找，最终发现地址5、地址6、地址7、地址8上存放的数都不是5，并且地址9的位置上没放数据，至此可知5不在这个哈希表里。
地址6，到第一个关键字为空的地址9需要比较4次，因此查找不成功的次数为4。
所以，查找不成功的平均查找长度为（3 + 2 + 1 + 2 + 1 + 5 + 4）/ 7 = 18 / 7。